Diferencia entre revisiones de «Geometría de tangram (Segundo)»
De WikiEducator
m |
|||
| Línea 5: | Línea 5: | ||
El [[tangram]] es una figura geométrica compleja que en una de sus configuraciones convexas es un gran cuadrado | El [[tangram]] es una figura geométrica compleja que en una de sus configuraciones convexas es un gran cuadrado | ||
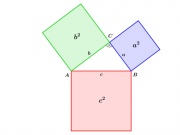
[[Archivo:Satz des Pytagoras n1.jpg|thumb|el teorema de Pitágoras permite deducir la hipotenusa, en la figura]] | [[Archivo:Satz des Pytagoras n1.jpg|thumb|el teorema de Pitágoras permite deducir la hipotenusa, en la figura]] | ||
| − | + | ||
[[File:Tangra 2b n1.jpg|thumb|[[paralelogramo]] ABE es [[congruente]] con DCE]] | [[File:Tangra 2b n1.jpg|thumb|[[paralelogramo]] ABE es [[congruente]] con DCE]] | ||
== Definición matemática== | == Definición matemática== | ||
| Línea 24: | Línea 24: | ||
{{Actividad|determine las áreas de las diversas figuras}} | {{Actividad|determine las áreas de las diversas figuras}} | ||
Nota: recuerde que la definición es pura algebra, no corresponde a una figura particular, como la que se diseño en la unidad [[Geometría de tangram]] | Nota: recuerde que la definición es pura algebra, no corresponde a una figura particular, como la que se diseño en la unidad [[Geometría de tangram]] | ||
| − | [[ | + | [[Archivo:Tangra o.png|thumb|left]] |
== Veáse también== | == Veáse también== | ||
Revisión de 06:32 15 oct 2022
| Describir las figuras geométricas |
El tangram es una figura geométrica compleja que en una de sus configuraciones convexas es un gran cuadrado
Definición matemática
- 2 triángulos rectos grandes (hipotenusa 1, lados √2/2 área 1/4)
- 1 triángulo recto mediano (hipotenusa √2/2, lados 1/2, área 1/8})
- 2 triángulos rectángulos chicos (hipotenusa 1/2, lados √2/4, área 1/16)
- 1 cuadrado (lados √2/4, área 1/8)
- 1 paralelogramo (lados de 1/2 y √2/4, área 1/8)
Material
- Lapices
- Escuadra
- Regla milimetrada o escalimetro
- Cuadriculado de 7mm
| Geometría de tangram |
| determine las áreas de las diversas figuras
|
Nota: recuerde que la definición es pura algebra, no corresponde a una figura particular, como la que se diseño en la unidad Geometría de tangram
Veáse también
Notas y referencias
- Weisstein, Eric W. "Parallelogram." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Parallelogram.html
Fuente
http://es.vikidia.org/wiki/Tangram
|
Trabajo en proceso, espera cambios frecuentes. Tu ayuda y retroalimentación son bienvenidos. Ver página de charlas. |
|
