ManuelRomero/grafica/presentacion
De WikiEducator
Revisión a fecha de 09:53 12 jun 2013; ManuelRomero (Discusión | contribuciones)
Saltar a: navegación, buscar
INFORMÁTICA GRÁFICA
¡Disfrutar aprendiendo ......!
El arte de modelar ...."
TRANSFORMACIÓN EN EL PIPELINE GRÁFICO
- Basado en un sistema de visualizacion
Objeto 3d ====>>> represntación en pantalla bidimensional
1.- Coordenadas del objeto (x,y,z,w)
Transformación ModelView
2.-Coordenadas del ojo
Proyección
TRANSFORMACIÓN EN EL PIPELINE GRÁFICO
3.- Cooredenadas de recorte
Perspectiva
4.-Coordenadas del dispositivo
Viewport
5.-Coordenadas de la ventana (x,y)
Trabajo a realizar
Coordenadadas del objeto
- Coordenadas globales o del mundo
- Coordenadas locales o del objeto
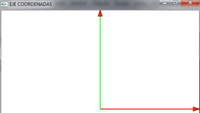
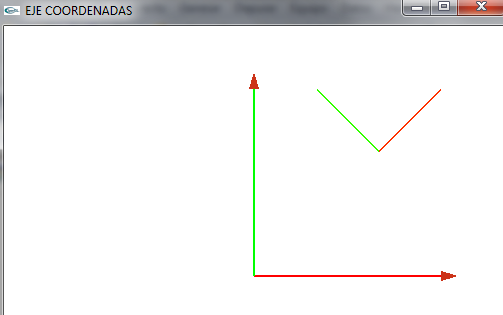
- Dibujamos un eje de coordenadas x,y,z.
- Estará centrado en el punto 0,0,0
Coordenadadas del objeto
- El código fuente
void dibujaCoordenadas(void){ porFlechitas(); glLineWidth(2); glBegin(GL_LINES); glLineWidth(3); glColor3f(1,0,0);//Eje X glVertex3f(0,0,0); glVertex3f(15,0,0); glColor3f(0,1,0);//Eje Y glVertex3f(0,0,0); glVertex3f(0,15,0); glColor3f(0,0,1);//Eje Z glVertex3f(0,0,0); glVertex3f(0,0,15); glLineWidth(1); glEnd(); glFlush(); }
Coordenadadas del objeto
- A OpenGL le especificamos bien por puntos o por vectores estos valores
- OpenGL rederiza en la pantalla y visualiza dichos puntos según le especifiquemos
Coordenadadas del objeto
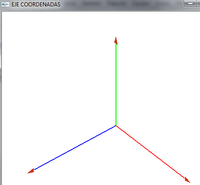
- giramos para ver mejor
- Lo giramos para ver la coordenada z. Esta parte luego la veremos
- Para conseguirlo he girado 40º en el eje de x y 40º en el eje de y
.. .. ..
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glRotatef(40.0f,1,0,0);
glRotatef(40.0f,0,1,0);
glutPostRedisplay();
.. .. ..Coordenadas del objeto
- Este eje de coordenadas que hemos dibujado representaría el eje de coordenadas del objeto
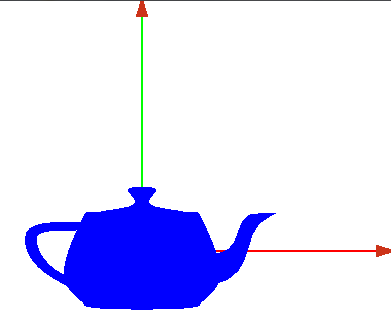
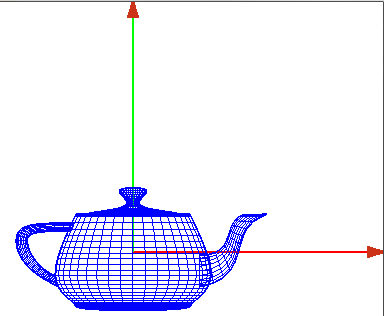
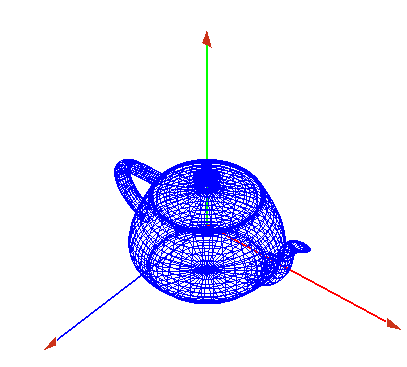
- Ahora dibujamos un objeto en él, por ejemplo una tetera
- con la barra espaciadora podemos cambiar su representación, sólida o de alambres
Eje de coordenadas del objeto
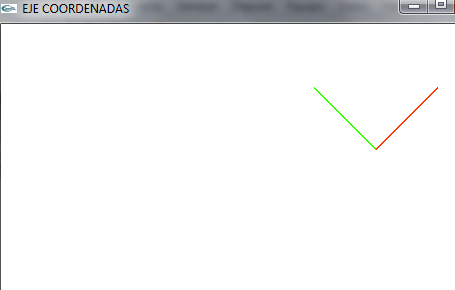
- Planteamos un nuevo eje de coordenadas
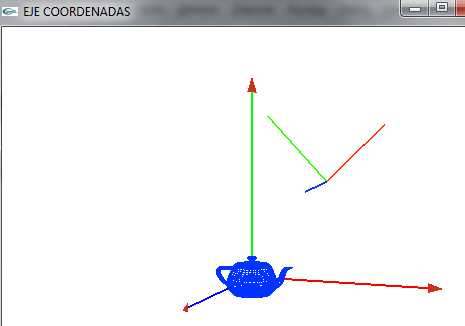
- Podemos ver que respecto al eje de coordenadas del mundo (0,0,0), tiene los siguientes vectores
(10,10,10)- (15,15,10) (10,10,10)- (5,15,10) (10,10,10)- (10,10,15)
- Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro
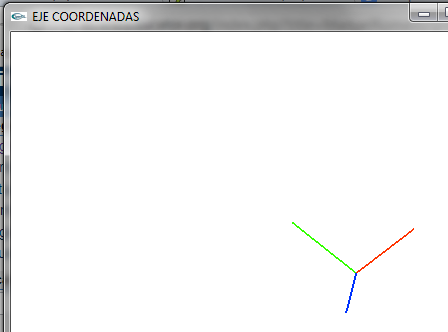
- Lo giramos para ver el componente z (Se observa en diferente posición pues lo he rotado respecto a X e Y de las coordenadas del mundo no de ella misma
- Lo giramos para verlo un poco mejor
- Vemos el objeto en el eje de coordenadas del mundo global y lo queremos pasar al eje de coordenadas del mundo local o del objeto
===Vamos a ver como pasar el objeto a las coordenadas locales
- Para ello vamos a multiplicar cada vétice del objeto por una matriz de escena
- Esta matriz permite realizar operaciones de rotación traslación y escalado
- En nuestro caso queremos coger la tetera y
- Trasladarla al punto 10,10,10.
- trasladar 10 unidades en X
- trasladar 10 unidades en Y
- trasladar 10 unidades en Z
- Rotar 15 grados
Son en total 4 operaciones