Diferencia entre revisiones de «ManuelRomero/grafica/escena1/objeto»
De WikiEducator
| (22 revisiones intermedias por el mismo usuario no mostrado) | |||
| Línea 1: | Línea 1: | ||
| − | {{:Usuario:ManuelRomero/grafica/escena1/nav}} | + | {{:Usuario:ManuelRomero/grafica/escena1/nav}} |
| − | <br> | + | <br> |
| + | {{#widget:Slides}} | ||
| − | = | + | <div class="slides layout-regular template-default"> |
| − | + | ||
| − | + | ||
| − | *Dibujamos un eje de coordenadas x,y,z. | + | <div class="slide"> |
| + | === Coordenadadas del objeto: '''''La matriz escena''''' === | ||
| + | Empezamos con dos tipos de coordenadas | ||
| + | #Coordenadas globales o del mundo | ||
| + | #Coordenadas locales o del objeto | ||
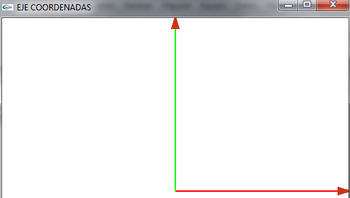
| + | *Dibujamos un eje de coordenadas x,y,z. | ||
*Estará centrado en el punto 0,0,0 | *Estará centrado en el punto 0,0,0 | ||
</div> | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| − | ===Coordenadadas del objeto=== | + | |
| + | === Coordenadadas del objeto === | ||
| + | |||
;El código fuente | ;El código fuente | ||
| − | <source lang=cpp> | + | <source lang="cpp"> |
void dibujaCoordenadas(void){ | void dibujaCoordenadas(void){ | ||
porFlechitas(); | porFlechitas(); | ||
| Línea 21: | Línea 27: | ||
glVertex3f(0,0,0); | glVertex3f(0,0,0); | ||
glVertex3f(15,0,0); | glVertex3f(15,0,0); | ||
| − | |||
glColor3f(0,1,0);//Eje Y | glColor3f(0,1,0);//Eje Y | ||
glVertex3f(0,0,0); | glVertex3f(0,0,0); | ||
| Línea 32: | Línea 37: | ||
glFlush(); | glFlush(); | ||
} | } | ||
| − | </source> | + | </source> |
</div> | </div> | ||
| − | <div class="slide"> | + | <div class="slide"> |
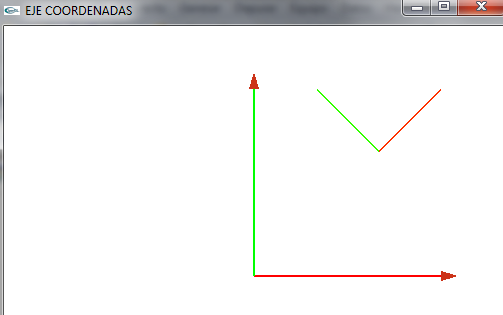
| − | === | + | === Veamos la imagen === |
| − | *A OpenGL le especificamos bien por puntos o por vectores estos valores | + | |
| + | *A OpenGL le especificamos bien por puntos o por vectores estos valores | ||
*OpenGL rederiza en la pantalla y visualiza dichos puntos según le especifiquemos | *OpenGL rederiza en la pantalla y visualiza dichos puntos según le especifiquemos | ||
| − | [[ | + | [[Image:CoordenadasOpenGLBásico.png|350px|center]] |
| − | </div> | + | </div> |
| + | |||
<div class="slide"> | <div class="slide"> | ||
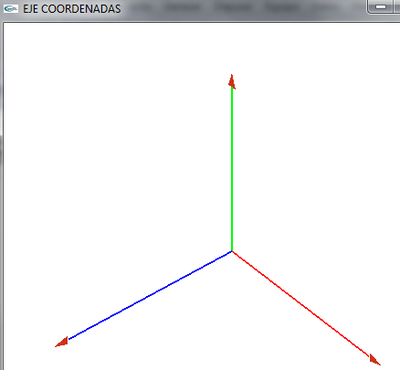
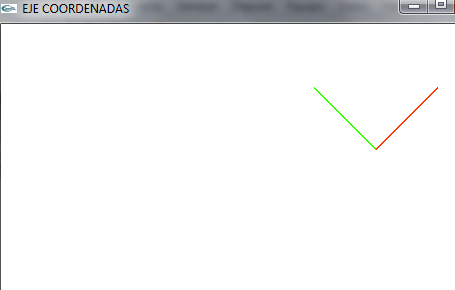
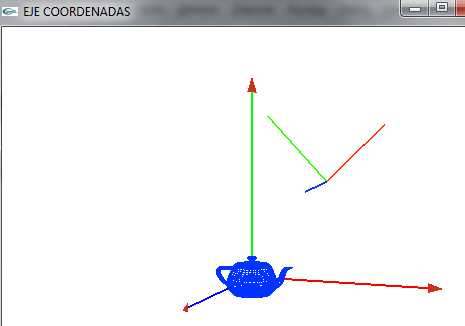
| − | === | + | === Giramos === |
| − | + | *Lo giramos para ver la coordenada z. Esta parte luego la veremos | |
| − | *Lo giramos para ver la coordenada z. Esta parte luego la veremos | + | *Para conseguirlo he girado 40º en el eje de '''''X''''' y 40º en el eje de '''''Y''''' |
| − | *Para conseguirlo he girado 40º en el eje de | + | <source lang="cpp"> |
| − | <source lang=cpp> | + | |
.. .. .. | .. .. .. | ||
glMatrixMode(GL_MODELVIEW); | glMatrixMode(GL_MODELVIEW); | ||
| Línea 53: | Línea 59: | ||
glutPostRedisplay(); | glutPostRedisplay(); | ||
.. .. .. | .. .. .. | ||
| − | </source> | + | </source> |
| − | </div> | + | </div> |
<div class="slide"> | <div class="slide"> | ||
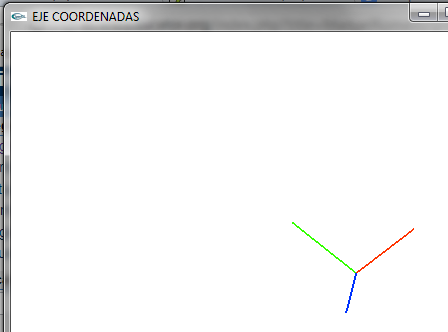
| − | ===Coordenadas del objeto=== | + | === Coordenadas del objeto === |
| − | [[ | + | *Vemos lo que sería las coordenadas del objeto |
| − | + | [[Image:CoordenadasOpenGL.png|400px|center]] | |
| − | + | ||
| − | + | ||
</div> | </div> | ||
| + | <div class="slide"> | ||
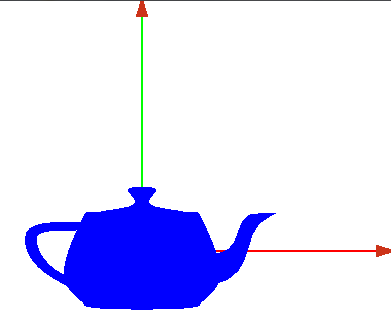
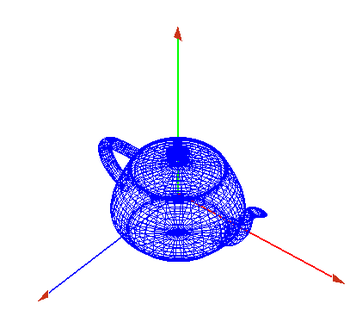
| + | ===Dibujando directamente=== | ||
| + | *Quitamos el giro y dibujamos una tetera | ||
| + | *Este eje de coordenadas que hemos dibujado representaría el eje de coordenadas del objeto | ||
| + | *Ahora dibujamos un objeto en él, por ejemplo una tetera | ||
| + | *Con la barra espaciadora podemos cambiar su representación, sólida o de alambres | ||
| + | <source lang=cpp> | ||
| + | case'2': | ||
| + | //quitamos el giro | ||
| + | glRotatef(40,0,1,0); | ||
| + | glRotatef(-30,1,0,0); | ||
| + | glutPostRedisplay(); | ||
| + | case '3': | ||
| + | //Dibujo la tetera | ||
| + | glutWireTeapot(3); | ||
| + | glFlush(); | ||
| + | break; | ||
| + | </source> | ||
| + | </div> - | ||
<div class="slide"> | <div class="slide"> | ||
*Representación sólida | *Representación sólida | ||
| − | [[ | + | [[Image:Tetera1.png|RTENOTITLE|center]] |
</div> | </div> | ||
| − | <div class="slide"> | + | <div class="slide"> |
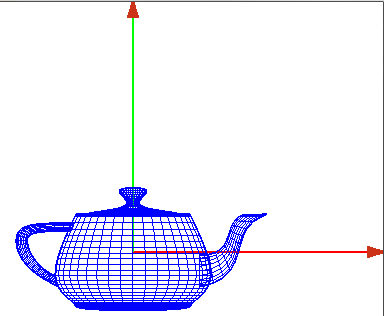
*Represetnación en alambres | *Represetnación en alambres | ||
| − | [[ | + | |
| − | </div> | + | [[Image:Tetera2.png|RTENOTITLE|center]] |
| + | </div> | ||
<div class="slide"> | <div class="slide"> | ||
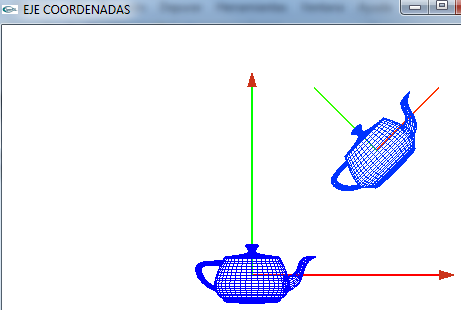
*Representación girada | *Representación girada | ||
| − | [[ | + | *Giramos en torno al eje X 20º y entorno al eje y 45º para tener una visión más de 3D. |
| − | *Ahora hemos dibujado la tetera respecto al eje de coordenadas del mundo | + | *Posteriormente se detallan estas operaciones |
| − | </div> | + | [[Image:Tetera3.png|RTENOTITLE|350px|center]] |
| + | *Ahora hemos dibujado la tetera respecto al eje de coordenadas del mundo con centro 0,0,0 | ||
| + | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| + | === Eje de coordenadas del objeto === | ||
| + | *En realidad el objeto está en una posición del espacio con sus coordenadas | ||
| + | *La idea es llevármelo a las coordenadas del mundo, para mi de referencia | ||
| + | *Planteamos este nuevo eje de coordenadas | ||
| + | *Podemos ver que respecto al eje de coordenadas del mundo (0,0,0), tiene los siguientes vectores | ||
| − | |||
| − | |||
| − | |||
(10,10,10)- (15,15,10) | (10,10,10)- (15,15,10) | ||
(10,10,10)- (5,15,10) | (10,10,10)- (5,15,10) | ||
(10,10,10)- (10,10,15) | (10,10,10)- (10,10,15) | ||
</div> | </div> | ||
| − | <div class="slide"> | + | <div class="slide"> |
| + | ===Coordenadas del objeto=== | ||
*Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro | *Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro | ||
| − | [[Image: | + | |
| + | [[Image:CoordenadasObjeto1.png|RTENOTITLE|center]] | ||
</div> | </div> | ||
| + | <div class="slide"> | ||
| + | ===Girando | ||
| + | *Lo giramos para ver el componente '''''Z''''' (Se observa en diferente posición pues lo he rotado respecto a X e Y de las coordenadas del mundo no de ella misma | ||
| + | |||
| + | [[Image:CoordenadasObjeto2.png|RTENOTITLE|center]] | ||
| + | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| − | * | + | ===Ambos ejes=== |
| − | [[Image: | + | *Vemos los dos ejes de coordenadas |
| + | |||
| + | [[Image:CoordenadasObjeto3.png|RTENOTITLE|center]] | ||
</div> | </div> | ||
| + | <div class="slide"> | ||
| + | ===Girando=== | ||
| + | *Lo giramos para verlo un poco mejor | ||
| + | *Vemos el objeto en el eje de coordenadas del mundo global y lo queremos pasar al eje de coordenadas del mundo local o del objeto | ||
| + | |||
| + | [[Image:CoordenadasObjeto4.png|RTENOTITLE]] | ||
| + | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| − | + | ===Paso de coordenadas=== | |
| − | + | *Vamos a ver como pasar el objeto a las coordenadas locales | |
| + | *Para ello vamos a multiplicar cada vértice del objeto por una''''' matriz de escena ''''' | ||
| + | *Esta matriz permite realizar operaciones de rotación traslación y escalado | ||
| + | *La operacion sería | ||
| + | '''''(X,Y,Z,W)'''''<sup>T</sup><sub>punto_de_vista</sub>='''''(X,Y,Z,W)'''''<sup>T</sup><sub>objeto</sub> * M<sub>mundo</sub>*''''' | ||
| + | </div> | ||
| + | |||
| + | <div class="slide"> | ||
| + | ===La matriz de escena=== | ||
| + | *Estas operaciones se realizan el OpenGL usando una matriz | ||
| + | *Cada vez que realizamos una operación de rotación, o de traslación estamos multiplicando por la matriz correspondiente | ||
| + | *En openGL especificamos que trabajamos con la matriz | ||
| + | <source lang=cpp> | ||
| + | .. .. .. | ||
| + | glMatrixMode(GL_MODELVIEW); | ||
| + | .. .. .. | ||
| + | </source> | ||
| + | *Al principio la matriz tiene el valor identidad 1 o elemento neutro | ||
</div> | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| − | + | ===Tipos de matrices=== | |
| − | * | + | *Tenemos dos tipos de matrices |
| − | + | *Esta es la matriz Modelo Vista | |
| + | *Hasta ahora hemos especificado la parte del modelo o de la escena con rotaciones y traslaciones | ||
| + | *Para realizar estas operaciones hemos usamos las primitivas de '''''openGL''''' | ||
| + | <source lang=cpp> | ||
| + | .. .. .. | ||
| + | glRotatef(alpha,x,y,z);//rota ''alpha'' grados entorno al eje especificado ''x,y,x'' | ||
| + | glTranslatef(x,y,z); //Traslada la imagen x,y,z | ||
| + | glScalef(sx,sy,xz);//Multiplica la matriz de escalado los factores sx,sy,xz. | ||
| + | .. .. .. | ||
| + | </source> | ||
</div> | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| − | === | + | ===Operaciones pasa pasar de coordenadas=== |
| − | + | *En nuestro caso queremos coger la tetera y | |
| − | + | #Trasladarla al punto 10,10,10. | |
| − | *En nuestro caso queremos coger la tetera y | + | ##trasladar 10 unidades en X |
| − | #Trasladarla al punto 10,10,10. | + | ##trasladar 10 unidades en Y |
| − | ##trasladar 10 unidades en X | + | ##trasladar 10 unidades en Z |
| − | ##trasladar 10 unidades en Y | + | #Rotar 45 grados |
| − | ##trasladar 10 unidades en Z | + | </div> |
| − | #Rotar 45 grados | + | <div class="slide"> |
| − | [[ | + | ===Operaciones=== |
| − | <source lang=cpp> | + | *Son en total 4 operaciones |
| + | [[Image:CoordenadasMundoObjeto.png|RTENOTITLE|center]] | ||
| + | <source lang="cpp"> | ||
.. ... .. | .. ... .. | ||
//Roto la tetera para llegar al eje de coordenadas del objeto | //Roto la tetera para llegar al eje de coordenadas del objeto | ||
| Línea 120: | Línea 193: | ||
glFlush(); | glFlush(); | ||
.. .. .. | .. .. .. | ||
| − | </source> | + | </source> |
| + | </div> | ||
| − | + | <div class="slide"> | |
| + | *Vemos ahora dos objetos y los desplazamos | ||
| + | [[Imagen:dosObjetos.png]] | ||
| + | *Los desplazamos | ||
| + | [[Imagen:dosObjetosDesplazados.png]] | ||
| + | </div> | ||
| + | <div class="slide"> | ||
| + | *Si solo queremos desplazar un objeto respecto a otro | ||
| + | *Entonces debemos mantener diferentes matrices de transformación a difernetes objetos de nuestra escena | ||
| + | *Dibujamos un objeto | ||
| + | *Lo desplazamos con M1 | ||
| + | *Recuperamos la matriz anterior | ||
| + | *La aplicamos a los nuevos objetos | ||
| + | *Lo vemos en las imágenes | ||
| + | </div> | ||
| + | <div class="slide"> | ||
| + | |||
| + | <gallery caption="Desplazamiento entre objetos"> | ||
| + | Imagen:desplazaObjeto1.png | ||
| + | Imagen:desplazaObjeto2.png | ||
| + | Imagen:desplazaObjeto3.png | ||
| + | Imagen:desplazaObjeto4.png | ||
| + | Imagen:desplazaObjeto5.png | ||
| + | </gallery> | ||
| + | </div> | ||
| + | <div class="slide"> | ||
| + | |||
| + | *OpenGL dispone de una pila para las matrices | ||
| + | *Para guardar/recuperar matrices: | ||
| + | glPushMatrix();//Guarda la matriz en la pila acutal | ||
| + | glPopMatriz();//Recupera la matriz de la pila. | ||
| + | *Estas funciones trabajan con la matriz actual. | ||
| + | </div> | ||
| + | <div class="slide"> | ||
| + | |||
| + | *El código asociado | ||
| + | <source lang=cpp> | ||
| + | void trasladaCubo(){ | ||
| + | static int i =0; | ||
| + | glClear(GL_COLOR_BUFFER_BIT); | ||
| + | glFlush(); | ||
| + | glColor3f(1,0,0); | ||
| + | glPopMatrix(); | ||
| + | glPushMatrix(); | ||
| + | dibujaCoordenadas(); | ||
| + | glutWireSphere(2,30,30); | ||
| + | glTranslatef(0,5+i++,0); | ||
| + | glutWireCube(2); | ||
| + | glFlush(); | ||
| + | } | ||
| + | </source> | ||
</div> | </div> | ||
<div class="slide"> | <div class="slide"> | ||
| − | {{ | + | {{Resumen| |
| − | + | *En la escena tengo unos objetos | |
| − | }} | + | *Cada uno tiene sus coordenadas ''coordenadas del objeto'' |
| + | *Paso estas coordenadas a las coordenadas del mundo | ||
| + | *Para ello multiplico por la matriz '''''M''''' que llamaremos ''matriz de escena'' | ||
| + | *Sistema de coordenadas en que se define la escena. Define cómo se colocan los diferentes objetos en la escena. | ||
| + | *La matriz de escena lleva movimientos de rotación traslación, giro, simetria, ... | ||
| + | }} | ||
| + | '''(X,Y,Z)'''<sub>mundo</sub> ='''(X,Y,Z)'''<sub>objeto</sub> * '''M'''<sub>escena</sub> | ||
</div> | </div> | ||
Última revisión de 11:10 13 jun 2013