Diferencia entre revisiones de «Plantilla:Bases Datos/Modelo Logico»
De WikiEducator
(Página creada con «===Nivel Lógico=== *A este nivel vamos a usar el '''''modelo relacional''''' *Es importante tener claro que lo que queremos realizar a este nivel es '''''aplicar una seri...») |
(→Conceptos del nivel lógico: Elementos del modelo) |
||
| Línea 33: | Línea 33: | ||
Se define como el papel que desempeña un determinado | Se define como el papel que desempeña un determinado | ||
dominio en una relación (tabla) | dominio en una relación (tabla) | ||
| − | [[Imagen: | + | [[Imagen:atributo_1.png]] |
*Podemos ver un dominio como un tipo de datos con restricciones. | *Podemos ver un dominio como un tipo de datos con restricciones. | ||
}} | }} | ||
| Línea 40: | Línea 40: | ||
*Se define como (no hace falta aprenderlo) | *Se define como (no hace falta aprenderlo) | ||
Un conjunto de pares de la forma | Un conjunto de pares de la forma | ||
| − | T = {(A1,D1),(A2,D2),....,(An,Dn)} | + | T <nowiki>={(A1,D1),(A2,D2),....,(An,Dn)}</nowiki> |
donde | donde | ||
| − | + | <nowiki> {A1,,A2,....,An} (n>0)</nowiki> es el conjunto de nombres de atributos del esquema necesariamente distintos. | |
| − | {D1,,D2,....,Dn} son los dominios asociados a dichos atributos que no tienen que ser necesariamente distintos. | + | <nowiki> {D1,,D2,....,Dn}</nowiki> son los dominios asociados a dichos atributos que no tienen que ser necesariamente distintos. |
}} | }} | ||
{{MRM_Definicion|Title=Relación| | {{MRM_Definicion|Title=Relación| | ||
| Línea 51: | Línea 51: | ||
Una relación es un conjunto de tuplas del mismo esquema , y un esquema de relación es el esquema de las tuplas que lo | Una relación es un conjunto de tuplas del mismo esquema , y un esquema de relación es el esquema de las tuplas que lo | ||
forman. Notación : | forman. Notación : | ||
| − | R (A1:D1, A2:D2, ....., An:Dn) | + | <nowiki> R (A1:D1, A2:D2, ....., An:Dn)</nowiki> |
| − | define una relación de esquema {(A1,D1),(A2,D2),....,(An,Dn)}. A partir de esta definición, diremos que dos | + | define una relación de esquema <nowiki> {(A1,D1),(A2,D2),....,(An,Dn)}.</nowiki> A partir de esta definición, diremos que dos |
relaciones R y S son compatibles si sus esquemas son idénticos. | relaciones R y S son compatibles si sus esquemas son idénticos. | ||
}} | }} | ||
{{MRM_Definicion|Title=Restricciones}} | {{MRM_Definicion|Title=Restricciones}} | ||
| − | |||
====Conceptos del nivel lógico: Dominio y atributo==== | ====Conceptos del nivel lógico: Dominio y atributo==== | ||
====Conceptos del nivel lógico: Dominio y atributo==== | ====Conceptos del nivel lógico: Dominio y atributo==== | ||
Revisión de 07:40 25 abr 2018
Contenido
Nivel Lógico
- A este nivel vamos a usar el modelo relacional
- Es importante tener claro que lo que queremos realizar a este nivel es aplicar una serie de reglas para transformar el modelo entidad/interrelación o modelo de Chen en un modelo relacional
|
Archivo:Tranformacion er mr.png
|
- En este nivel hay que estudiar una serie de conceptos sencillos, que convienen dejar claros
Conceptos del nivel lógico: Elementos del modelo
Un dominio es el conjuntos de valores que puede tomar un determinado atributo (campo). de un elemento concreto (tupla o fila) del objeto (relación o tabla).
|
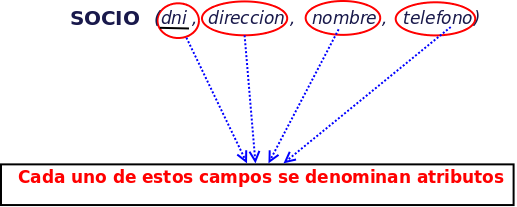
Un atributo son cada una de las características o propiedades de los elementos de información (tablas) Se define como el papel que desempeña un determinado dominio en una relación (tabla)
|
Un conjunto de pares de la forma T ={(A1,D1),(A2,D2),....,(An,Dn)} donde {A1,,A2,....,An} (n>0) es el conjunto de nombres de atributos del esquema necesariamente distintos. {D1,,D2,....,Dn} son los dominios asociados a dichos atributos que no tienen que ser necesariamente distintos. |
Una relación es un conjunto de tuplas del mismo esquema , y un esquema de relación es el esquema de las tuplas que lo forman. Notación : R (A1:D1, A2:D2, ....., An:Dn) define una relación de esquema {(A1,D1),(A2,D2),....,(An,Dn)}. A partir de esta definición, diremos que dos
relaciones R y S son compatibles si sus esquemas son idénticos.
|