Coordenadas del ojo:La matriz punto de vista

• Ahora tenemos el objeto respecto a una coordenadas del mundo
• Tenemos que poner el ojo en alguna posicion de la escena
• Para ello colocamos una cámara y hacemos una foto desde esa posición
• Esta metáfora permite representar la forma en la que openGL va a represtar la escena dependiendo del punto de vista
• La cámara son nuestros ojos virtuales

Definición

Las coordenadas del ojo define la escena respecto al punto de vista de la cámara

(X,Y,Z,W)^T_{punto_de_vista}=(X,Y,Z,W)^T * M_mundo* </div>

• Para hacer esto en openGL, disponemos de la funcion

void gluLookAt(eyeX, eyeY, eyeZ, cenX,cenY,cenZ, atX, atY,atZ);

• Esta función determina dónde y cómo está dispuesta la cámara.
• Antes de llamar a esta función debe estar activa la matriz ModeloVista
• Esta función se aplica sobre la matriz ModeloVista

M=M_escena * M_{punto_vista}

Uso de la función gluLookAt(...)

Esta función tiene tres grupos de parámetros

void gluLookAt(GLdouble eyeX,GLdouble eyeY,GLdouble eyeZ,GLdouble centerX,GLdouble centerY,GLdouble centerZ,GLdouble upX,GLdouble upY,GLdouble upZ);

punto eyeX, eyeY, eyeZ

• Es el punto central donde ponemos nuestra cámara ficticia.

punto centerX,centerY,centerZ

• Es el punto hacia donde miramos

Sería el vector formado por los puntos   ojo-center

vector upX,upY,upZ

Este vector permite girar la cámara
Es perpendicular al vector hacia donde miramos

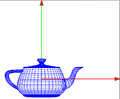
• Vamos a llevar este ejemplo a la práctica
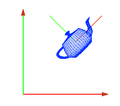
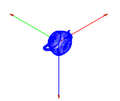
• Si tenemos nuestro eje de coordenadas y queremos mirar desde el punto 10,10,10 hacia el 0,0,0
• En cada imagen vamos cambiando la oreientación de la cámara
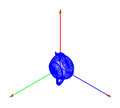
  • 10,0,0
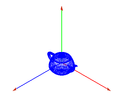
  • 0,10,0
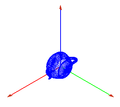
  • 0,0,10

• El código de cada una de estas imágenes
• Respecto al eje X

  //Ponemos un punto de vista respecto al eje X
  glMatrixMode(GL_MODELVIEW);
  glClear(GL_COLOR_BUFFER_BIT);
  glPopMatrix();
  glPushMatrix();
  gluLookAt(10,10,10,0,0,0,10,0,0);
  dibujaCoordenadas();
  glutWireTeapot(3);
  glFlush();

• Respecto al eje Y

  //Ponemos un punto de vista respecto al eje X
  glMatrixMode(GL_MODELVIEW);
  glClear(GL_COLOR_BUFFER_BIT);
  glPopMatrix();
  glPushMatrix();
  gluLookAt(10,10,10,0,0,0,0,10,0);
  dibujaCoordenadas();
  glutWireTeapot(3);
  glFlush();

• Respecto al eje Z

  //Ponemos un punto de vista respecto al eje X
  glMatrixMode(GL_MODELVIEW);
  glClear(GL_COLOR_BUFFER_BIT);
  glPopMatrix();
  glPushMatrix();
  gluLookAt(10,10,10,0,0,0,0,0,10);
  dibujaCoordenadas();
  glutWireTeapot(3);
  glFlush();

Otro punto de vista

• Ahora vamos a poner el punto de vista donde estaba el objeto en un principio
• En las coordenadas del objeto
• Y miraremos a nuestro objeto llevado al centro 0,0,0

• El código lleva dos acciones
• Primero dibujo los ejes de corrdenadas (local y global) o del mundo y del objeto opcion b
• Después pongo establezco con la función gluLookAt(..) las coordenadas del punto de vista
• Y desde ahí observo el objeto opción c

  case'b':
    //Respecto al eje del donde estaba el objeto
	 glClear(GL_COLOR_BUFFER_BIT);
	 dibujaCoordenadas();
	 dibujaCoordenadasObjeto();
	 glFlush();
	 break;
  case'c':
  //Esta opción que se ejecuta después de b
	 glClear(GL_COLOR_BUFFER_BIT);
	 glMatrixMode(GL_MODELVIEW);
	 glPopMatrix();
	 glPushMatrix();
	 gluLookAt(10,10,10,0,0,0,5,5,0);
     	 dibujaCoordenadas();
	 glutWireTeapot(3);
	 glFlush();
         break;