Diferencia entre revisiones de «ManuelRomero/grafica/escena1/objeto»
De WikiEducator
(→Eje de coordenadas del objeto) |
|||
| Línea 78: | Línea 78: | ||
===Eje de coordenadas del objeto=== | ===Eje de coordenadas del objeto=== | ||
| − | *Planteamos | + | *En realidad el objeto está en una posición del espacio con sus coordenadas |
| + | *La idea es llevármelo a las coordenadas del mundo, para mi de referencia | ||
| + | *Planteamos este nuevo eje de coordenadas | ||
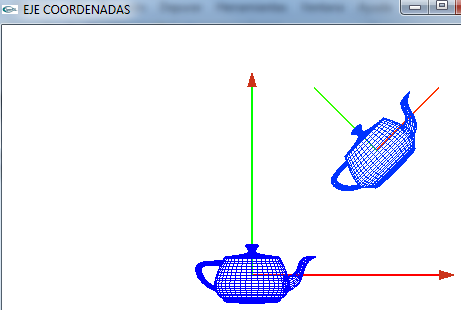
*Podemos ver que respecto al eje de coordenadas del mundo (0,0,0), tiene los siguientes vectores | *Podemos ver que respecto al eje de coordenadas del mundo (0,0,0), tiene los siguientes vectores | ||
(10,10,10)- (15,15,10) | (10,10,10)- (15,15,10) | ||
| Línea 111: | Línea 113: | ||
##trasladar 10 unidades en Z | ##trasladar 10 unidades en Z | ||
#Rotar 45 grados | #Rotar 45 grados | ||
| + | |||
| + | Son en total 4 operaciones | ||
[[Imagen:CoordenadasMundoObjeto.png]] | [[Imagen:CoordenadasMundoObjeto.png]] | ||
<source lang=cpp> | <source lang=cpp> | ||
| Línea 121: | Línea 125: | ||
.. .. .. | .. .. .. | ||
</source> | </source> | ||
| + | {{Resumen|En la escena tengo unos objetos | ||
| + | Cada uno tiene sus coordenadas | ||
| + | Paso estas coordenadas a las coordenadas del mundo | ||
| + | Para ello multiplico por la matriz M de escena | ||
| + | (x,y,z)mundo = (x,y,z)objeto M escena | ||
| + | <math>(x,y,z)_{mudo}=(X,Y,Z)_{objeto} * M_{escena}</math> | ||
| − | + | Sistema de coordenadas en que se define la escena. Define cómo se colocan los diferentes objetos en la escena. | |
| + | |||
| + | |||
| + | (x, y, z, w)T mundo = (x, y, z, w)Tobjeto ·Mescena | ||
| + | |||
| + | |||
| + | |||
| + | Mescena pasa de coordenadas objeto a coordenadas mundo (rotaciones, translaciones, escalados… ) | ||
| + | }} | ||
</div> | </div> | ||
<div class="slide"> | <div class="slide"> | ||
Revisión de 11:25 12 jun 2013
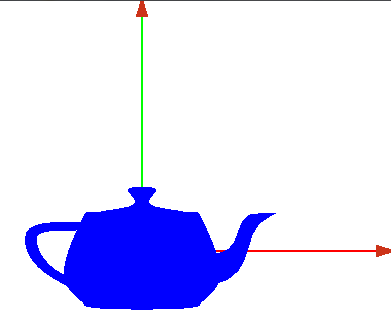
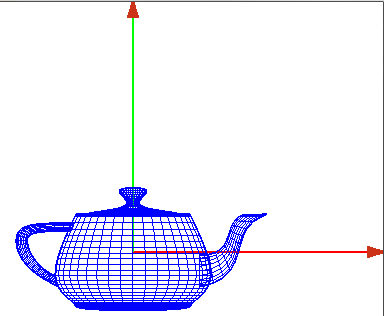
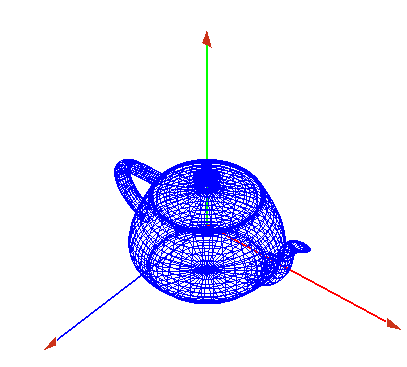
Coordenadadas del objeto
- Coordenadas globales o del mundo
- Coordenadas locales o del objeto
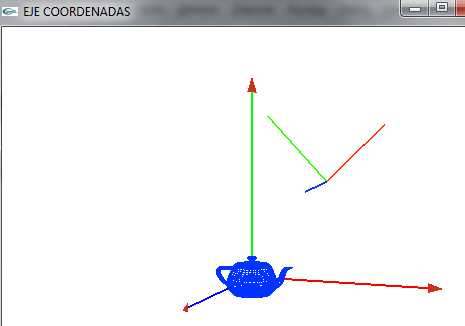
- Dibujamos un eje de coordenadas x,y,z.
- Estará centrado en el punto 0,0,0
</div>