Diferencia entre revisiones de «ManuelRomero/grafica/presentacion»

De WikiEducator
Saltar a: navegación, buscar
Línea 26: Línea 26:
 
<div class="slide">
 
<div class="slide">
 
===Trabajo a realizar===
 
===Trabajo a realizar===
−
{{Objetivo|*Realizaremos una escena de una tetera e iremos viendo todo el proceso de transforación que se va produciendo con OpenGL.}}
+
{{Objetivo|
 +
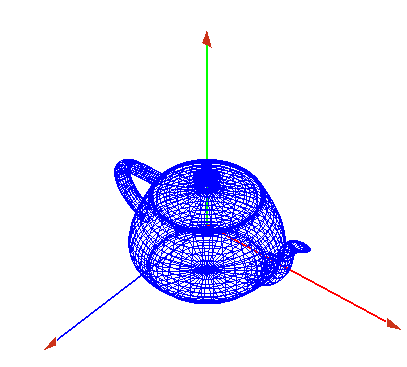
#Realizaremos una escena de una '''''tetera'''''
 +
#en el proceso de visualización  iremos viendo todo el proceso de transforación que se va produciendo con OpenGL.
 +
#Realizaremos un seguimiento de '''''la pipeline gráfica'''''}}
 
</div>
 
</div>
 +
<div class="slide">
 +
===Coordenadadas del objeto===
 +
#Coordenadas globales o del mundo
 +
#Coordenadas locales o del objeto
  
−
===Coordenadas globales - coordenadas locales===
 
 
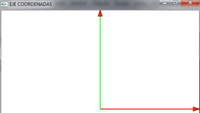
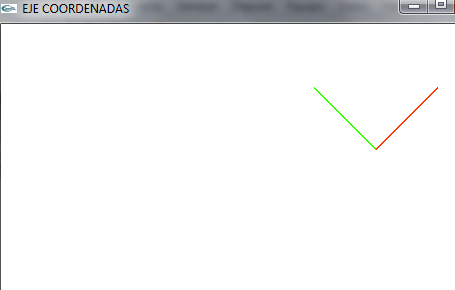
*Dibujamos un eje de coordenadas x,y,z.
 
*Dibujamos un eje de coordenadas x,y,z.
 
*Estará centrado en el punto 0,0,0
 
*Estará centrado en el punto 0,0,0
 +
</div>
 +
<div class="slide">
 +
===Coordenadadas del objeto===
 +
;El código fuente
 
<source lang=cpp>
 
<source lang=cpp>
 
void dibujaCoordenadas(void){
 
void dibujaCoordenadas(void){
Línea 53: Línea 63:
 
}
 
}
 
</source>
 
</source>
 +
</div>
 +
<div class="slide">
 +
===Coordenadadas del objeto===
 
*A OpenGL le especificamos bien por puntos o por vectores estos valores
 
*A OpenGL le especificamos bien por puntos o por vectores estos valores
 
*OpenGL rederiza en la pantalla y visualiza dichos puntos según le especifiquemos
 
*OpenGL rederiza en la pantalla y visualiza dichos puntos según le especifiquemos
−
 
 
[[Imagen:CoordenadasOpenGLBásico.png|200px]]
 
[[Imagen:CoordenadasOpenGLBásico.png|200px]]
 +
</div>
 +
<div class="slide">
 +
===Coordenadadas del objeto===
 +
;giramos para ver mejor
 
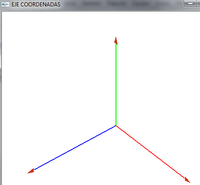
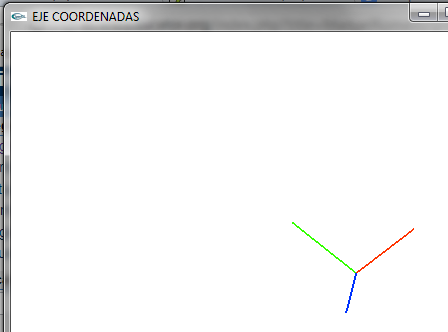
*Lo giramos para ver la coordenada z. Esta parte luego la veremos
 
*Lo giramos para ver la coordenada z. Esta parte luego la veremos
−
*PAra conseguirlo he girado 40º en el eje de x y 40º en el eje de y  
+
*Para conseguirlo he girado 40º en el eje de x y 40º en el eje de y  
 
<source lang=cpp>
 
<source lang=cpp>
 
   .. .. ..
 
   .. .. ..
Línea 68: Línea 84:
 
   .. .. ..
 
   .. .. ..
 
</source>
 
</source>
 +
</div>
 +
<div class="slide">
 +
===Coordenadas del objeto===
 
[[Imagen:CoordenadasOpenGL.png|200px]]
 
[[Imagen:CoordenadasOpenGL.png|200px]]
 
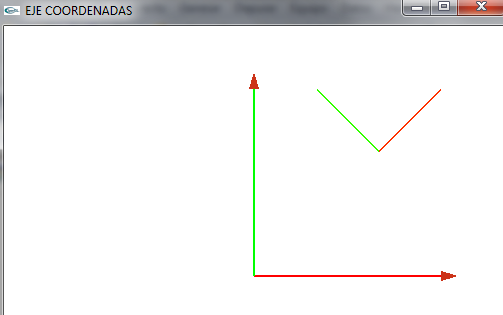
*Este eje de coordenadas que hemos dibujado representaría el eje de coordenadas del objeto
 
*Este eje de coordenadas que hemos dibujado representaría el eje de coordenadas del objeto
 
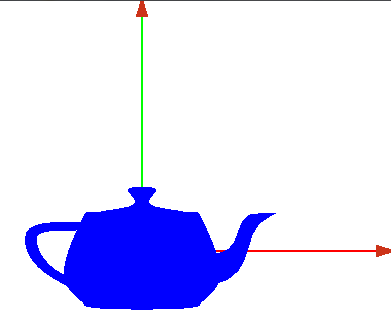
*Ahora dibujamos un objeto en él, por ejemplo una tetera
 
*Ahora dibujamos un objeto en él, por ejemplo una tetera
 
*con la barra espaciadora podemos cambiar su representación, sólida o de alambres
 
*con la barra espaciadora podemos cambiar su representación, sólida o de alambres
 +
</div>
 +
<div class="slide">
 
*Representación sólida
 
*Representación sólida
 
[[Imagen:tetera1.png]]
 
[[Imagen:tetera1.png]]
 +
</div>
 +
<div class="slide">
 
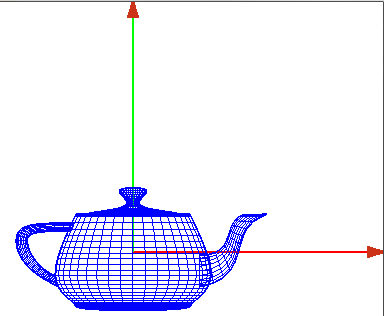
*Represetnación en alambres
 
*Represetnación en alambres
 
[[Imagen:tetera2.png]]
 
[[Imagen:tetera2.png]]
 +
</div>
 +
<div class="slide">
 
*Representación girada
 
*Representación girada
 
[[Imagen:tetera3.png]]
 
[[Imagen:tetera3.png]]
 
*Ahora hemos dibujado la tetera respecto al eje de coordenadas del mundo
 
*Ahora hemos dibujado la tetera respecto al eje de coordenadas del mundo
 +
</div>
 +
<div class="slide">
  
 
===Eje de coordenadas del objeto===
 
===Eje de coordenadas del objeto===
Línea 86: Línea 113:
 
  (10,10,10)- (5,15,10)
 
  (10,10,10)- (5,15,10)
 
  (10,10,10)- (10,10,15)
 
  (10,10,10)- (10,10,15)
 +
</div>
 +
<div class="slide">
 
*Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro
 
*Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro
 
[[Image:coordenadasObjeto1.png]]
 
[[Image:coordenadasObjeto1.png]]
 +
</div>
 +
<div class="slide">
 
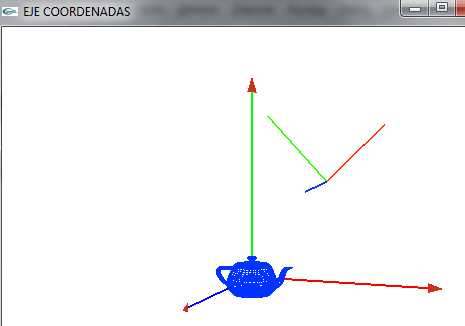
*Lo giramos para ver el componente z (Se observa en diferente posición pues lo he rotado respecto a X e Y de las coordenadas del mundo no de  ella misma
 
*Lo giramos para ver el componente z (Se observa en diferente posición pues lo he rotado respecto a X e Y de las coordenadas del mundo no de  ella misma
 
[[Image:coordenadasObjeto2.png]]
 
[[Image:coordenadasObjeto2.png]]
 +
</div>
 +
<div class="slide">
 
*Vemos los dos ejes de coordenadas
 
*Vemos los dos ejes de coordenadas
 
[[Image:coordenadasObjeto3.png]]
 
[[Image:coordenadasObjeto3.png]]
 +
</div>
 +
<div class="slide">
 
*Lo giramos para verlo un poco mejor  
 
*Lo giramos para verlo un poco mejor  
 
*Vemos el objeto en el eje de coordenadas del mundo global  y lo queremos pasar al eje de coordenadas del mundo local o del objeto
 
*Vemos el objeto en el eje de coordenadas del mundo global  y lo queremos pasar al eje de coordenadas del mundo local o del objeto
 
[[Image:coordenadasObjeto4.png]]
 
[[Image:coordenadasObjeto4.png]]
 +
</div>
 +
<div class="slide">
 
===Vamos a ver como pasar el objeto a las coordenadas locales
 
===Vamos a ver como pasar el objeto a las coordenadas locales
 
*Para ello vamos a multiplicar cada vétice del objeto por una matriz de escena
 
*Para ello vamos a multiplicar cada vétice del objeto por una matriz de escena
Línea 105: Línea 142:
 
#Rotar 15 grados  
 
#Rotar 15 grados  
 
Son en total 4 operaciones
 
Son en total 4 operaciones
−
 
+
</div>
 +
<div class="slide">
 
{{Recursos de la Web|
 
{{Recursos de la Web|
 
http://asanchez.cs.buap.mx/arreglos_vertices.pdf
 
http://asanchez.cs.buap.mx/arreglos_vertices.pdf
 
}}
 
}}
−
 
+
</div>
 +
<!--
  
  
Línea 190: Línea 229:
 
}
 
}
 
</source>
 
</source>
 +
-->

Revisión de 09:53 12 jun 2013



TRANSFORMACIÓN EN EL PIPELINE GRÁFICO

  • Basado en un sistema de visualizacion 
Objeto 3d ====>>> represntación en pantalla bidimensional

1.- Coordenadas del objeto (x,y,z,w) 

  Transformación ModelView

2.-Coordenadas del ojo 

 Proyección

TRANSFORMACIÓN EN EL PIPELINE GRÁFICO

3.- Cooredenadas de recorte 

Perspectiva

4.-Coordenadas del dispositivo 

 Viewport

5.-Coordenadas de la ventana (x,y)

Trabajo a realizar

Icon objectives.jpg

Objetivo

  1. Realizaremos una escena de una tetera
  2. en el proceso de visualización iremos viendo todo el proceso de transforación que se va produciendo con OpenGL.
  3. Realizaremos un seguimiento de la pipeline gráfica

Coordenadadas del objeto

  1. Coordenadas globales o del mundo
  2. Coordenadas locales o del objeto
  • Dibujamos un eje de coordenadas x,y,z.
  • Estará centrado en el punto 0,0,0

Coordenadadas del objeto

El código fuente 
void dibujaCoordenadas(void){
	porFlechitas();
	glLineWidth(2);
	glBegin(GL_LINES);
	   glLineWidth(3);
	   glColor3f(1,0,0);//Eje X
	   glVertex3f(0,0,0);
	   glVertex3f(15,0,0);
 
	   glColor3f(0,1,0);//Eje Y
	   glVertex3f(0,0,0);
	   glVertex3f(0,15,0);
       glColor3f(0,0,1);//Eje Z
	   glVertex3f(0,0,0);
	   glVertex3f(0,0,15);
	   glLineWidth(1);
	glEnd();
	glFlush();
}

Coordenadadas del objeto

  • A OpenGL le especificamos bien por puntos o por vectores estos valores
  • OpenGL rederiza en la pantalla y visualiza dichos puntos según le especifiquemos

CoordenadasOpenGLBásico.png

Coordenadadas del objeto

giramos para ver mejor
  • Lo giramos para ver la coordenada z. Esta parte luego la veremos
  • Para conseguirlo he girado 40º en el eje de x y 40º en el eje de y 
  .. .. ..
    glMatrixMode(GL_MODELVIEW);
    glLoadIdentity();   
    glRotatef(40.0f,1,0,0);
    glRotatef(40.0f,0,1,0);
    glutPostRedisplay();
  .. .. ..

Coordenadas del objeto

CoordenadasOpenGL.png

  • Este eje de coordenadas que hemos dibujado representaría el eje de coordenadas del objeto
  • Ahora dibujamos un objeto en él, por ejemplo una tetera
  • con la barra espaciadora podemos cambiar su representación, sólida o de alambres
  • Representación sólida

Tetera1.png

  • Represetnación en alambres

Tetera2.png

  • Representación girada

Tetera3.png

  • Ahora hemos dibujado la tetera respecto al eje de coordenadas del mundo

Eje de coordenadas del objeto

  • Planteamos un nuevo eje de coordenadas
  • Podemos ver que respecto al eje de coordenadas del mundo (0,0,0), tiene los siguientes vectores 
(10,10,10)- (15,15,10)
(10,10,10)- (5,15,10)
(10,10,10)- (10,10,15)
  • Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro

CoordenadasObjeto1.png

  • Lo giramos para ver el componente z (Se observa en diferente posición pues lo he rotado respecto a X e Y de las coordenadas del mundo no de ella misma

CoordenadasObjeto2.png

  • Vemos los dos ejes de coordenadas

CoordenadasObjeto3.png

  • Lo giramos para verlo un poco mejor
  • Vemos el objeto en el eje de coordenadas del mundo global y lo queremos pasar al eje de coordenadas del mundo local o del objeto

CoordenadasObjeto4.png

===Vamos a ver como pasar el objeto a las coordenadas locales

  • Para ello vamos a multiplicar cada vétice del objeto por una matriz de escena
  • Esta matriz permite realizar operaciones de rotación traslación y escalado
  • En nuestro caso queremos coger la tetera y
  1. Trasladarla al punto 10,10,10.
    1. trasladar 10 unidades en X
    2. trasladar 10 unidades en Y
    3. trasladar 10 unidades en Z
  2. Rotar 15 grados

Son en total 4 operaciones


Icon inter.gif

Recursos de la Web

http://asanchez.cs.buap.mx/arreglos_vertices.pdf


Obtenido de «https://es.wikieducator.org/index.php?title=ManuelRomero/grafica/presentacion&oldid=13313»