Diferencia entre revisiones de «ManuelRomero/grafica/presentacion»
De WikiEducator
(→Eje de coordenadas del objeto) |
|||
| Línea 86: | Línea 86: | ||
Viewport | Viewport | ||
#Coordenadas de la ventana (x,y) | #Coordenadas de la ventana (x,y) | ||
| − | ===Coordenadas | + | ===Coordenadas globales - cooredenadas locales=== |
*Dibujamos un eje de coordenadas x,y,z | *Dibujamos un eje de coordenadas x,y,z | ||
<source lang=cpp> | <source lang=cpp> | ||
| Línea 139: | Línea 139: | ||
*Vemos el objeto en el eje de coordenadas del mundo global y lo queremos pasar al eje de coordenadas del mundo local o del objeto | *Vemos el objeto en el eje de coordenadas del mundo global y lo queremos pasar al eje de coordenadas del mundo local o del objeto | ||
[[Image:coordenadasObjeto4.png]] | [[Image:coordenadasObjeto4.png]] | ||
| + | ===Vamos a ver como pasar el objeto a las coordenadas locales | ||
| + | *Para ello vamos a multiplicar cada vétice del objeto por una matriz de escena | ||
| + | *Esta matriz permite realizar operaciones de rotación traslación y escalado | ||
| + | *En nuestro caso queremos coger la tetera y | ||
| + | #Trasladarla al punto 10,10,10. | ||
| + | ##trasladar 10 unidades en X | ||
| + | ##trasladar 10 unidades en Y | ||
| + | ##trasladar 10 unidades en Z | ||
| + | #Rotar 15 grados | ||
| + | Son en total 4 operaciones | ||
Revisión de 01:51 12 jun 2013
Esqueleto de un programa openGL
#include <GL/glut.h> // Drawing routine. void escena(void) { glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); // Clear the buffers including // the depth buffer. glPolygonMode(GL_FRONT, GL_FILL); glBegin(GL_TRIANGLE_STRIP); glEnd(); // Write labels. glFlush(); } // Initialization routine. void setup(void) { glClearColor(1.0, 1.0, 1.0, 0.0); } // OpenGL window reshape routine. void redibuja(int w, int h) { glViewport(0, 0, (GLsizei)w, (GLsizei)h); glMatrixMode(GL_PROJECTION); glLoadIdentity(); glOrtho(0.0, 100.0, 0.0, 100.0, -1.0, 1.0); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); } // Keyboard input processing routine. void teclado(unsigned char key, int x, int y) { switch(key) { case ' ': case 27: default: break; } } // Routine to output interaction instructions to the C++ window. void printInteraction(void) { cout << "Interaction:" << endl; cout << "Press the space bar to toggle between wirefrime and filled for the lower annulus." << endl; } // Main routine. int main(int argc, char **argv) { printInteraction(); glutInit(&argc, argv); glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH); // Initialize the buffers // including the depth buffer. glutInitWindowSize(500, 500); glutInitWindowPosition(100, 100); glutCreateWindow("circularAnnuluses.cpp"); setup(); glutDisplayFunc(escena); glutReshapeFunc(redibuja); glutKeyboardFunc(teclado); glutMainLoop(); return 0; }
TRANSFORMACIÓN EN EL PIPELINE GRÁFICO
- Coordenadas del objeto (x,y,z,w)
Transformación ModelView
- Coordenadas del ojo
Proyección
- Cooredenadas de recorte
Perspectiva
- Coordenadas del dispositivo
Viewport
- Coordenadas de la ventana (x,y)
Coordenadas globales - cooredenadas locales
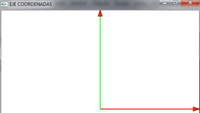
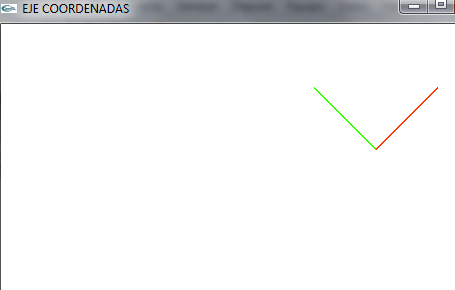
- Dibujamos un eje de coordenadas x,y,z
void dibujaCoordenadas(void){ porFlechitas(); glLineWidth(2); glBegin(GL_LINES); glLineWidth(3); glColor3f(1,0,0);//Eje X glVertex3f(0,0,0); glVertex3f(15,0,0); glColor3f(0,1,0);//Eje X glVertex3f(0,0,0); glVertex3f(0,15,0); glColor3f(0,0,1);//Eje z glVertex3f(0,0,0); glVertex3f(0,0,15); glLineWidth(1); glEnd(); glPushMatrix(); glFlush(); }
- Así quedaría
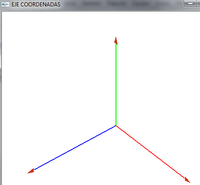
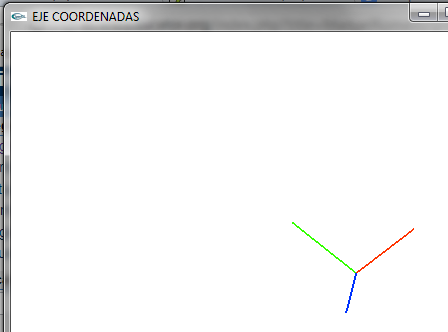
- Lo giramos para ver la coordenada z
- Este eje de coordenadas que hemos dibujado representaría el eje de coordenadas del objeto
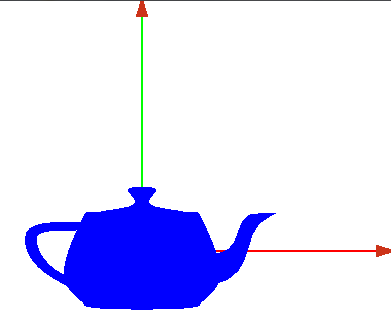
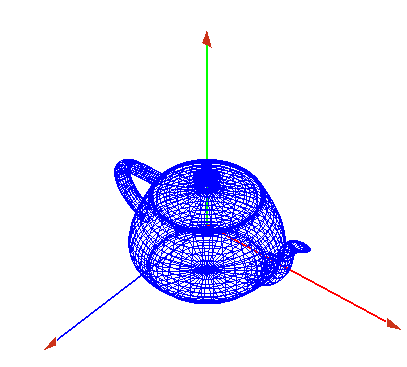
- Ahora dibujamos un objeto en él, por ejemplo una tetera
- con la barra espaciadora podemos cambiar su representación, sólida o de alambres
- Representación sólida
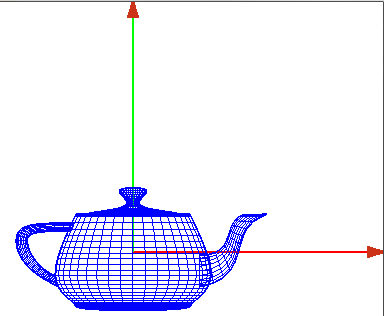
- Represetnación en alambres
- Representación girada
- Ahora hemos dibujado la tetera respecto al eje de coordenadas del mundo
Eje de coordenadas del objeto
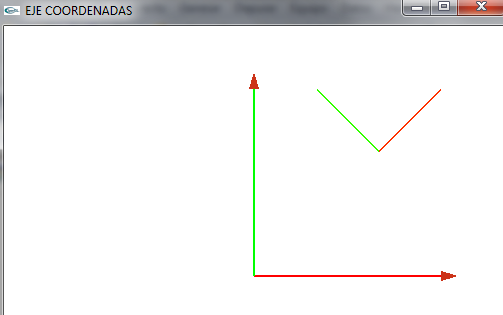
- Planteamos un nuevo eje de coordenadas
- Podemos ver que respecto al eje de coordenadas del mundo (0,0,0), tiene los siguientes vectores
(10,10,10)- (15,15,10) (10,10,10)- (5,15,10) (10,10,10)- (10,10,15)
- Gráficamente lo podemos ver en la imagen (siempre respecto al eje de coordenadas de nuestro mundo (0,0,0) como centro
- Lo giramos para ver el componente z (Se observa en diferente posición pues lo he rotado respecto a X e Y de las coordenadas del mundo no de ella misma
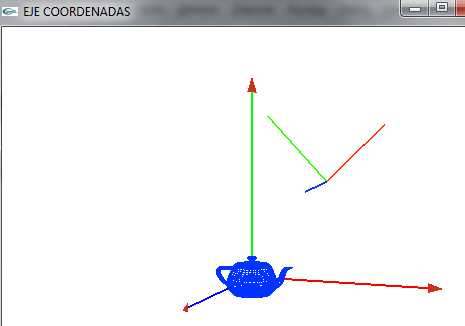
- Vemos los dos ejes de coordenadas
- Lo giramos para verlo un poco mejor
- Vemos el objeto en el eje de coordenadas del mundo global y lo queremos pasar al eje de coordenadas del mundo local o del objeto
 ===Vamos a ver como pasar el objeto a las coordenadas locales
===Vamos a ver como pasar el objeto a las coordenadas locales
- Para ello vamos a multiplicar cada vétice del objeto por una matriz de escena
- Esta matriz permite realizar operaciones de rotación traslación y escalado
- En nuestro caso queremos coger la tetera y
- Trasladarla al punto 10,10,10.
- trasladar 10 unidades en X
- trasladar 10 unidades en Y
- trasladar 10 unidades en Z
- Rotar 15 grados
Son en total 4 operaciones