Diferencia entre revisiones de «Recta por dos puntos»
De WikiEducator
m (Archivo:Dos ptos área graf.png) |
(br) |
||
| Línea 32: | Línea 32: | ||
En la formula P' tiene coordenadas (x´,y´) y P<sup>2</sup> tiene coordenadas (x<sup>2</sup>,y<sup>2</sup> | En la formula P' tiene coordenadas (x´,y´) y P<sup>2</sup> tiene coordenadas (x<sup>2</sup>,y<sup>2</sup> | ||
<ref>Larsen, H. D. 1953 Rinehart Mathematical Tables, formulas and curves. p. 208 Holt, Rinehart and Winston New York, Chicago San Francisco, Toronto, London ISBN 03-008915-8</ref> | <ref>Larsen, H. D. 1953 Rinehart Mathematical Tables, formulas and curves. p. 208 Holt, Rinehart and Winston New York, Chicago San Francisco, Toronto, London ISBN 03-008915-8</ref> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
===Información para ejercitar=== | ===Información para ejercitar=== | ||
| Línea 37: | Línea 47: | ||
pares 7,12; 1,0 | pares 7,12; 1,0 | ||
pares 1,0; 2,2 | pares 1,0; 2,2 | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
{{actividad|cálculo de notas, en escala 1-7, para 12 puntos}} | {{actividad|cálculo de notas, en escala 1-7, para 12 puntos}} | ||
Revisión de 09:59 31 may 2013
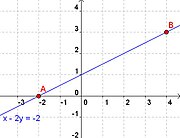
| trazar una recta dado dos puntos |
material
- papel cuadriculado
- crayones
- lapices de color
- regla milimetrada
| revisa el video
|
| deduzca la nota con siete puntos
|
- método del trazado
- método de cálculo de la recta
Material para calcular
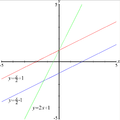
- formula : y=m.x+t
donde m: es la pendiente
relación del largo de la linea negra vs gris
[1] y el intercepto es t
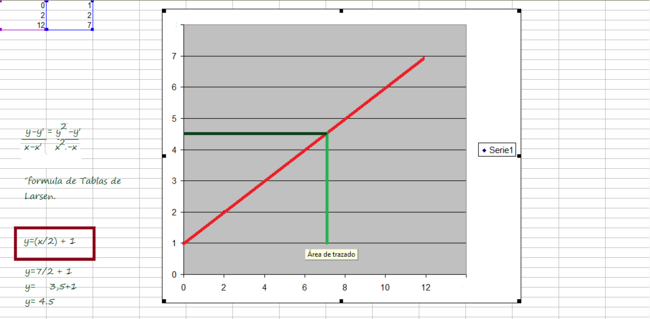
Formula para dos puntos
y-y' /(x-x')= y2-y'/(x2-x')
En la formula P' tiene coordenadas (x´,y´) y P2 tiene coordenadas (x2,y2
[2]
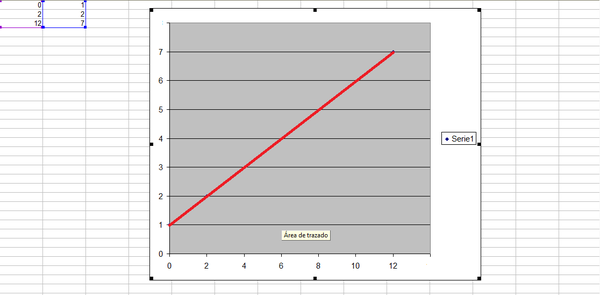
Información para ejercitar
pares 7,12; 1,0
pares 1,0; 2,2
| cálculo de notas, en escala 1-7, para 12 puntos
|
Notas
- ↑ http://profelenafreire.shoutwiki.com/wiki/Coeficiente_angular
- ↑ Larsen, H. D. 1953 Rinehart Mathematical Tables, formulas and curves. p. 208 Holt, Rinehart and Winston New York, Chicago San Francisco, Toronto, London ISBN 03-008915-8
